森林与二叉树:数据结构中的转化之美
在计算机科学中,各种数据结构其独特的方式帮助我们高效地存储和管理信息。其中,森林和二叉树是两种广泛使用的数据结构。森林是一组彼此独立的树,而二叉树则是一种特定的树形结构,每个节点最多只能有两个子节点。将森林转化为二叉树,不仅能提高数据存储的效率,还能为进一步的数据处理提供便利。本文将深入解析这一高效数据结构的转化过程,揭示其所带来的优势。
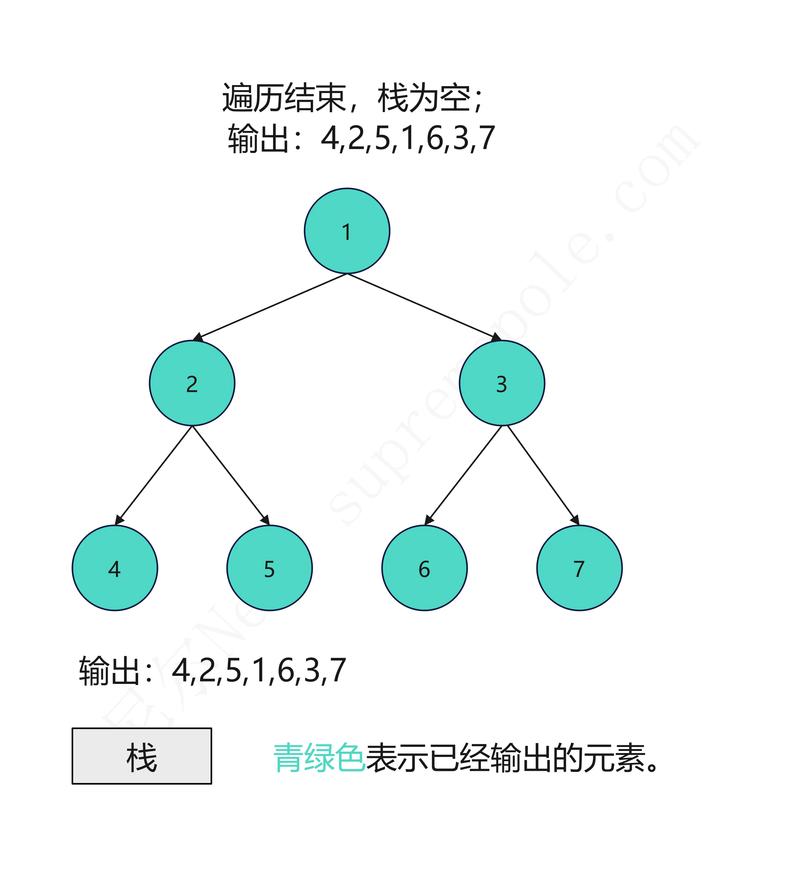
森林的概念与特征
我们需要理解什么是森林。在计算机科学中,森林是多个不相交的树的。在森林中,每棵树都可以看作是一个独立的数据结构。森林的特点包括:
- 结构灵活:森林可以包含任意数量的树。
- 树的层次分明:每棵树都有一个根节点,且节点之间的层次关系清晰。
- 适用范围广:森林常用于表示多种多样的关系,如家谱、组织结构等。
二叉树的基本特征
二叉树是一种特殊的树形结构,具有以下基本特征:
- 每个节点最多有两个子节点,通常称为左子节点和右子节点。
- 二叉树的高度即为其最大层次,影响着其存取时间。
- 在二叉排序树中,左子树的值总是小于或等于父节点的值,右子树的值总是大于父节点的值。
将森林转化为二叉树的策略
理解了森林和二叉树的基本概念后,接下来将讨论如何将森林高效地转化为二叉树。转化的方法通常有以下步骤:
- 选取根节点:遍历森林中的每棵树,选取每棵树的根节点作为二叉树的新根节点。
- 链接子树:将每棵树的左子节点设置为新的二叉树的左子节点,而将其右子节点设置为该树的右子树的根节点。
- 递归处理:对每一个子树重复以上步骤,直到所有的树都被链接到二叉树中。
这种转换方法充分利用了二叉树的结构特,使得每棵树的层次信息得以保留,减少了空间浪费。
森林转化为二叉树的优势
将森林转化为二叉树,我们可以享受到以下几个优势:
- 简化数据处理:二叉树结构简单,有助于加快查找和遍历的速度。
- 节省内存空间:在某些情况下,转化后的二叉树在内存占用方面更为高效。
- 更好的支持算法:许多经典的算法(如查找、排序)可以直接应用于二叉树,提升了数据操作的灵活。
将森林转化为二叉树不仅是一个优雅的数据结构转换过程,更是提升计算效率的有效手段。在现代计算机应用中,合理选用和转换数据结构是算法优化的关键之一。本文的探讨,相信读者对森林与二叉树之间的关系有了更深入的理解,也能在实践中更好地应用这些知识,为高效的数据处理铺平道路。










