三个矢量叉乘运算法则,矢量叉乘三则全解析
在物理和工程学中,矢量是一种重要的数学工具,而矢量的叉乘作为一种常用的运算,更是广泛应用于力学、电磁学等领域。叉乘不仅能够计算出两个矢量之间的关系,还可以几个基本法则来简化复杂的计算。本文将为您全面解析三个矢量叉乘的运算法则,帮助您更深入地理解这一重要的数学概念。
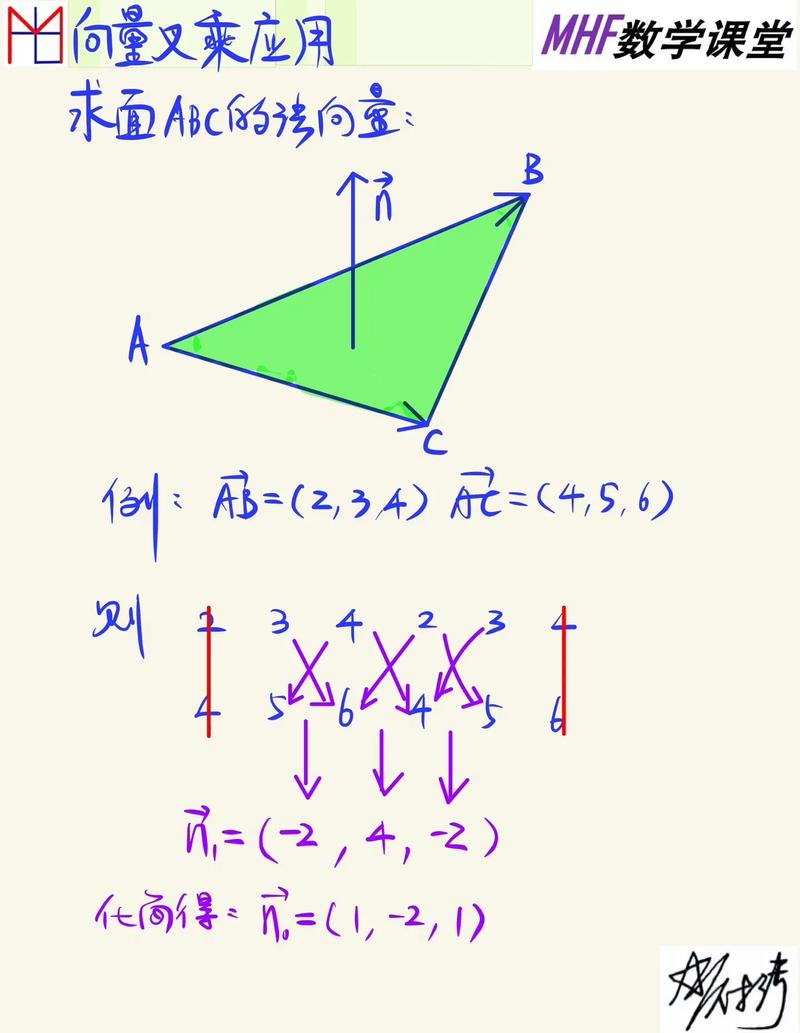
什么是矢量叉乘?
矢量叉乘(cross product)是用于计算两个三维矢量的运算,结果是一个与这两个矢量都垂直的新矢量。其表达式为:如果有两个矢量 **A** 和 **B**,那么它们的叉乘可以表示为 **A × B**。叉乘的结果不仅与 **A** 和 **B** 的大小有关,还和它们之间的夹角密切相关。具体而言,**A × B** 的大小等于 **A** 和 **B** 的大小乘以它们夹角的正弦值。
叉乘的第一个法则:反交换法则
叉乘的第一个基本法则是反交换法则,即对于任意两个矢量 **A** 和 **B**,都有:
A × B = - (B × A)
这条法则表明,交换两个矢量的顺序会导致结果的方向发生反转。这一点在物理学中具有重要的意义,例如,在力的计算中,力的施加方向与反作用力之间的关系正体现了这一法则。
叉乘的第二个法则:结合法则
叉乘的第二个法则称为结合法则,其表述为对于任意矢量 **A**, **B** 和 **C**,有:
A × (B × C) = (A · C) B - (A · B) C
这一法则允许我们在处理多个矢量的情况下,运用已知矢量之间的关系进行简化推导,从而提高计算效率。在物理现象建模中,这一法则常用于计算合成力和合成运动等问题。
叉乘的第三个法则:线法则
叉乘的第三个法则是线法则,它说明了在提供一个矢量的线组合情况下如何进行叉乘运算。其表述为:
A × (kB + C) = k(A × B) + A × C
这里的 **k** 是一个标量系数。这条法则表明,叉乘操作在矢量的加法和数乘上是线的。这一质在处理更复杂的矢量场和多物理场作用时非常有用,可以帮助我们更快速地得到结果。
以上三个矢量叉乘法则的解析,我们不仅加深了对矢量叉乘的理解,也为后续的复杂数学和物理计算奠定了基础。这些法则的应用可以极大地简化我们的计算过程,提高解决实际问题的效率。无论是在学术研究还是在工程实践中,理解并掌握这些基本法则都是至关重要的。
我们希望此次的解析,您能够更清晰地掌握矢量的叉乘运算,利用这些法则在实际应用中游刃有余。矢量的世界丰富多彩,等待我们不断探索与发现!










