2×2列联表卡方检验:理解和计算方法
当我们需要了解两个变量之间是否存在关联时,可以使用列联表卡方检验。在这种情况下,我们通常使用2×2列联表卡方检验。本文将详细介绍2×2列联表卡方检验的计算方法和意义。
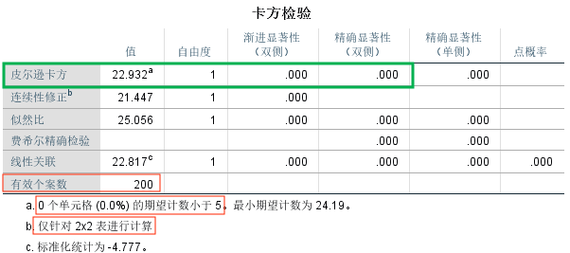
公式推导
2×2列联表卡方检验的计算公式如下:
卡方值 = (|ad-bc|^2) * n / [(a+b)(c+d)(a+c)(b+d)]
其中,a、b、c、d 分别代表四个不同单元格的观察频数,n表示总样本容量。
卡方值的解释
卡方值表示观察值与期望值之间的差异程度。通常,卡方值越大,表示两个变量之间的关联越显著。我们将卡方值与卡方分布表进行比较,以确定是否拒绝原假设。如果卡方值大于卡方分布表中的临界值,则我们可以拒绝原假设,认为两个变量之间存在显著的关联。
计算示例
假设我们有如下的2×2列联表:
| 变量A | 非变量A | |
|---|---|---|
| 变量B | a | b |
| 非变量B | c | d |
假设观察频数为:a=50, b=30, c=20, d=40。总样本容量为n=140。
根据上述数据,我们可以计算卡方值:
卡方值 = (|(50*40)-(30*20)|^2) * 140 / [(50+30)(20+40)(50+20)(30+40)]
卡方值 = (800)^2 * 140 / [(80)(60)(70)(70)]
卡方值 = 320000 * 140 / 23520000
卡方值 ≈ 1910.256
根据卡方分布表,我们可以找到卡方值为1910.256对应的显著水平。如果显著水平小于设定的阈值(通常为0.05),我们可以拒绝原假设,表明变量A和变量B之间存在显著的关联。
以上示例,我们可以看到2×2列联表卡方检验是一种简单且有效的统计方法,用于确定两个变量之间是否存在关联。计算卡方值并与卡方分布表进行比较,我们可以得出并作出合适的决策。希望本文对2×2列联表卡方检验的理解和实践有所帮助。
关键词:2×2列联表卡方检验、公式推导、计算方法、意义










